Wolfram Alpha Cellular Automaton - The Coding Train Challenge #179

This is my entry to the coding train challenge #179 "wolfram alpha - CA".

The challenge was to build a simple cellular automaton that operates in only one dimension.

See the original video from from the coding train
Read more about Elementary Cellular Automata

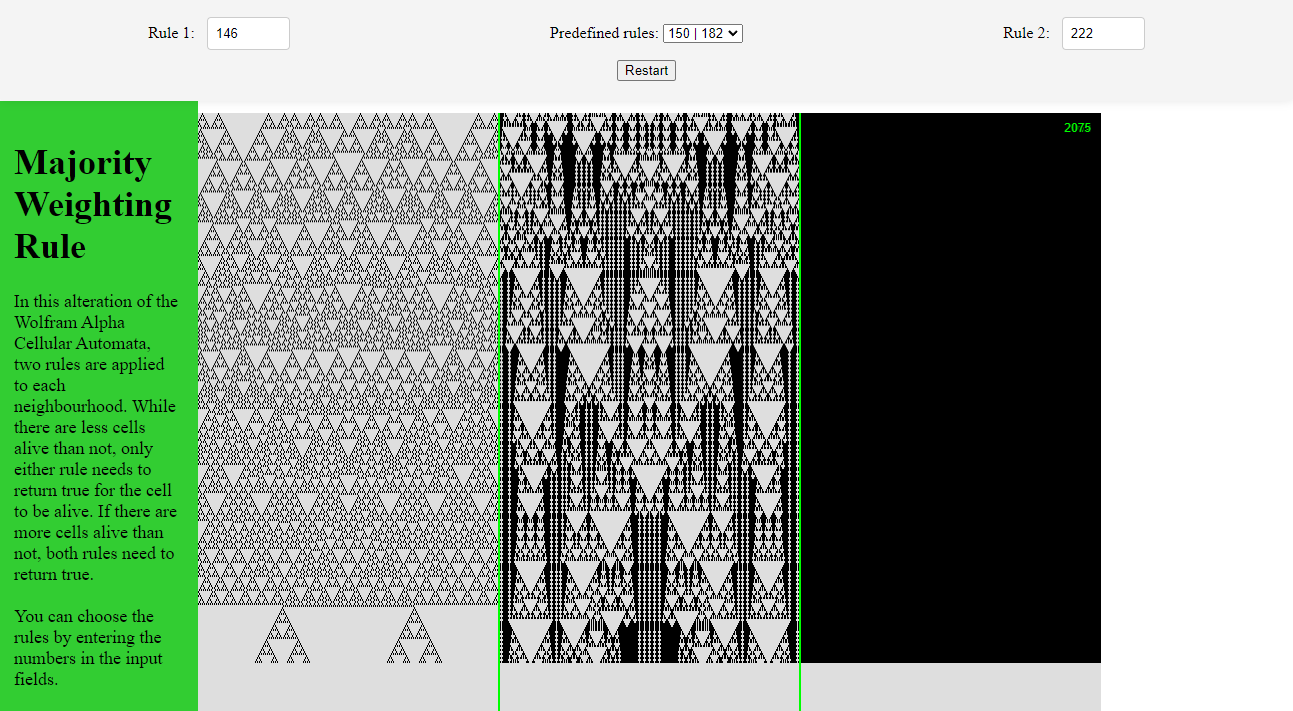
So the idea behind my entry was to play around with the ruleset of the cellular automaton.
What i ended up doing was basically adding the state of an entire row as part of the input for the next generation.

The 'global' state is defined by checking if the majority of cells in the current row are active or not.
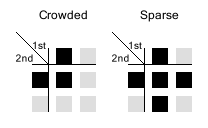
Let's call that state 'sparse' for few active cells and 'crowded' for many active cells.

const alive_count = this.current_state.cells.reduce((a, b): number => a + b.value, 0); 
const global_state = alive_count > (this.current_state.cells.length / 2) ? 'crowded' : 'sparse';

Now if the new state of a cell should be determined base on the current neighbourhood we first apply two (distinct) regular rules for elementary cellular automata. Based on the 'global' state and the results we then decide the state of the new cell.
For a 'crowded' state both rules need to result in an active cell for the final result to return active.
For a 'sparce' state both either rule needs to result in an active cell for the final result to return active.

switch (global_state) {
  case 'crowded': return rule1 && rule2;
  case 'sparse': return rule1 || rule2;
}

This leads to more 'stable' environments, where it is less likely that all cells assume the same state.
Rules in this automata are defined by the first and the second sub-rule they apply.
As an example an update step in Rule "30 - 54" would look like this.